En la ejecución de proyectos de infraestructura puede surgir imprevistos durante el desarrollo de una obra, por ejemplo, retrasos en completar algún hospital, carretera o escuela, pero ¿sabemos por qué se dan estas demoras? Los proyectos de infraestructura tienen una naturaleza compleja, lo que implica que pueden acontecer hechos que causen que la ejecución de un proyecto no se apegue a lo planificado, haciendo que demore más de lo estimado y cueste más de lo presupuestado. Por eso, es importante examinar el rol de la supervisión en obras de infraestructura, ya que es un elemento clave en la identificación de riesgosa, así como en el seguimiento de indicadores de calidad a lo largo del proyecto, además de una adecuada comunicación de resultados a través de los informes de supervisión.
Este tipo de situaciones no se podrían respaldar sin la experiencia de los expertos, quienes se apoyan de sólidas bases estadísticas para la toma de decisiones basadas en evidencia, cuyo principal insumo son los datos.
Cabe señalar que, el sector de la construcción de obras de infraestructura vial produce mucha información que debe ser gestionada, organizada y simplificada, además de estar orientada a una digitalización y sistematización. Sólo de esta forma, los procesos con los que se interactúa día con día en el sector darán cumplimiento óptimo a los resultados esperados en los proyectos.
Existe una forma analítica de predecir estos eventos relevantes de la ejecución; extensiones de costos y plazos. El inicio de la respuesta la encontramos en la estadística inferencial, cuya disciplina emergente cobra cada vez más relevancia en distintos ámbitos de las políticas públicas y la gestión de proyectos. En la División de Transporte del BID hemos aplicado la ciencia de los datos para desarrollar algoritmos de Machine y Deep Learning y poder obtener productos analíticos de fenómenos observables, que nos permitan ir un paso adelante en la predicción de posibles escenarios que perjudiquen la buena ejecución de proyectos en la región, a través de buenas prácticas con soporte estadístico.
Una de las metodologías de análisis de datos convencional es el cálculo de los intervalos de confianza, definido como un rango de valores derivado de los estadísticos de la muestra. Este instrumento de análisis se utiliza para evaluar la estimación del parámetro de población. En este sentido, se usa para comparar la media de las extensiones de plazo en los contratos de obra, con el objetivo de comprobar de qué forma se comportan los diferentes proyectos de rehabilitación, mantenimiento y ampliación de carreteras.
Por ejemplo, si tomamos una muestra aleatoria de proyectos durante 6 meses, en los que las extensiones de plazo en 15 países tienen una media de 0.34 meses (diez días) y el intervalo de confianza central de 95% es 0.83 (en una escala de 0 a 1), esto significa que hay un amplio margen de confianza y se puede concluir que existe un 95% de certeza que la extensión de plazo media de todos los contratos se encuentre entre ocho y doce días.
El siguiente gráfico muestra la variación de intervalos de confianza de extensiones de plazo de la población total de 280 contratos durante seis meses. Es Importante resaltar el ligero aumento de contratos con extensiones menores a dos meses.
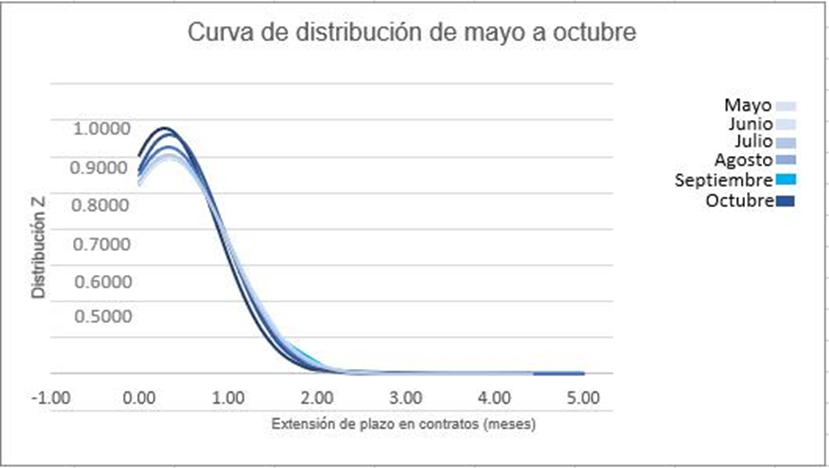
Asimismo, otra metodología aplicada es el análisis de varianzas (ANOVA), que se refiere al conjunto de datos Anova single factor data set, también llamado one-way, que permite descartar hipótesis nulas o alternativas referentes a medias muestrales. Es preciso ajustar la significancia para evitar hacer comparaciones erróneas.
De este modo, se realizó un experimento aplicado a una muestra aleatoria de contratos de obra en tres países en el mes de noviembre del 2020. El objetivo fue comprobar cuál es la varianza de extensión de plazo de estos contratos, con la finalidad de entender la interacción de los datos y definir aritméticamente si existe diferencia significativa en la muestra.
Al realizar este experimento, se asume que existe igualdad de varianzas esperando que el p-value (o valor p) sea significativo.
Este parámetro estadístico sirve para aceptar o descartar hipótesis nulas e hipótesis alternativas entre dos variables.
El resultado del p-value en el conjunto de datos para los tres países revela que la extensión de plazo es de 0.27 (desviación estándar), por lo tanto, no hay variación significativa, aunque las medias son similares. La siguiente gráfica de cajas muestra la variación de extensiones de plazo de los contratos de los tres países. La línea en el centro de las cajas representa la mediana. La hipótesis nula asume que no existe variación significativa entre las extensiones de plazo en los meses analizados.
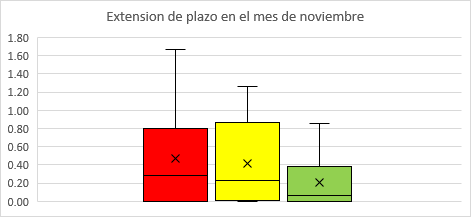
En conclusión, podemos decir que, a través de este tipo de metodologías, se puede conocer el estado de ejecución de proyectos de infraestructura. La estadística exploratoria, tiene el fin de diagnosticar fenómenos que permitan crear estrategias para la toma de decisiones orientadas a mitigar riesgos. La exploración de los datos es y será siempre una herramienta que nos permita entender el presente analizando el pasado, para predecir un mejor futuro. Importante resaltar las palabras del director del Centro de Ciencias de Datos Espaciales de la Universidad de Chicago “Los datos son minas de oro de los eventos que nos ocurren”.


Muchas gracias por la informacipon, es muy importante el uso estadistico de la información para poder tomar decisiones, para optimizar la ejecución de los proyectos de infraestructura,.
Por favor me podria indicar como poder tener acceso al estudio de las estadisticas completas de los intervalos de confianza y del anova elaborado para poder profundizar mis conocimientos, muchas gracias.